Основные законы логики в полном составе – все 10 штук. Законы логики от Аристотеля, Лейбница, Клавия, Пирса, де Моргана. Пусть ваша логика станет безупречной!
Логика – наука, ориентированная на познавательную деятельность человечества. В поле ее зрения находятся и самые разнообразные формы мышления, и возникающие в мыслительном процессе отношения между ними. Считается, что есть женская логика, есть мужская, но в действительности логическое мышление не разграничивается по половому принципу, так как мыслительным процессом управляют одни и те же законы.
Для чего нужна логика? Чтобы грамотно, последовательно и эффективно доносить свою позицию до собеседника. Без соответствующих умений делать это очень непросто. В своей речи вы должны последовательно и непротиворечиво излагать свою позицию, не забывая о логических связках между высказываниями. Последнее особенно важно, так как «Попытка нарушить закон природы способна убить вас, но точно так же попытка нарушить закон логики убивает в вас разум», — заявлял в свое время Александр Леонидович Никифоров, известный деятель науки, философ и теоретик.
Далее мы познакомим вас не только с тремя законами логики, открытыми еще древнегреческим мыслителем Аристотелем (закон тождества, закон (запрета) противоречия, закон исключенного третьего), но и с законом достаточного оснвания Лейбница, а также соответствующими математическими открытия в области логики, сделанными другими учеными – в общей сложности до 10!
Первые четыре из законов логики, которые мы рассмотрим, определяются, как формальные и называются основными. Углубляясь немного в историю, отметим, что под логическим законом еще Аристотель понимал предпосылку к объективным, заложенным природой, правильным размышлениям.
Сегодня под термином Логический закон понимается существенная, сокрытая внутри высказывания необходимая связь между логическими формами, обнаруживающая себя по ходу построения рассуждения. Для наглядности, основные законы логики принято записывать в виде соответствующих формул. Они часто встречаются в учебниках, всевозможных пособиях и научных трудах, но сами ученые называют их определенную условность, так как они лишь схематично обозначают сущность законов логики.
I. Закон тождества. Когда мысль равна сама себе
В тексте «Метафизики» Аристотель подчеркивал, что размышление в принципе нельзя осуществить (оно будет несостоятельным) «если каждый раз не мыслить что-нибудь одно». Сегодня эта фраза излагается несколько иначе. В учебных материалах по логике распространено такое определение: «Любое высказывание (суждение, мысль, а также понятие) неукоснительно должно сохранять один и тот же смысл в течение всего рассуждения».
Современные нам исследователи подчеркивают, что различные мысли запрещается принимать за тождественные, а тождественные за различные. Дело в том, что в обычной речи (особенно при пересказе) зачастую кажется, будто без труда можно выразить одну мысль другими словами. Это очень опасное заблуждение, так как в результате оно может привести к замене одной мысли другой (то есть изначальный смысл будет полностью утерян).
Рассмотрим случаи нарушения закона тождества на примерах:
А) Ученики прослушали объяснение учителя
Б) На турнире рассеянный шахматист много раз терял очки
Видите, как ярко, очевидно нарушается закон тождества во фразе под номером А. Обратить внимание нужно на словосочетание «ученики прослушали». С одной стороны школьники могли внимательно ВЫСЛУШАТЬ преподавателя, а с другой — пропустить все сказанное им мимо ушей. Получается, что из-за малейшего нюанса меняется смысл всей фразы.
Аналогично от нас ускользает смысл предложения «На турнире рассеянный шахматист много раз терял очки». Без дополнительной информации мы не можем понять – те ли очки он терял, которые присуждают успешным спортсменам, или те, которые у него на носу?! Вот так и выходит, что тождественными друг другу представляются в рамках одной фразу сразу две ситуации – одна трагическая, а другая комическая.
Необходимость применения при построении логических фраз закона тождества Аристотель обосновал, обратившись к софизмам (это такие высказывания, которые, если не вдумываться, кажутся верными, однако в сути своей ложные). Вот несколько софизмов, в которых нарушается закон тождества:
А) 8 и 5 это нечетное и четное числа. При этом в совокупности 8 и 5 равняются 13. То есть 13 это одновременно нечетное и четное число.
Б) То, что наполовину наполнено – наполовину пусто. Раз половины равны, то равны и целые части. То есть полное это тоже, что и пустое.
Если рассмотреть все представленные выше примеры, то можно проследить, что несмотря на кажущуюся верность рассуждений во всех случаях нарушен закон тождества. Если разобрать пример А, то видно, что один и тот же союз в двух первых предложениях (союз «и») имеет разное значение. Вначале он носит объединяющий характер (в значении «и то и другое»), в затем недвусмысленно указывает на факт сложения двух чисел. Так и выходит – раз в процессе размышлений к одному предмету (или к слову, как в нашем случае) применялись разные смыслы. В результате имеем нарушение закона логики – то есть в целом высказывание неверно.
Всякий софизм в своей сути (даже весьма тонкий) построен по накатанной дорожке – в них всегда не очень заметно соотносятся совершенно нетождественные друг с другом предметы или ситуации, события и высказывания. При этом соблюдается внешняя правдоподобность таких «неправдивых» фраз.
Опасайтесь софистов в обычной жизни, то и дело нарушающих законы тождества и порою стремящихся обвести вас вокруг пальца. Особенно популярен софизм в телевизионной и прочей рекламе товаров и услуг. Как вам такой софизм?:
Ответь, что круче: жизнь в раю после смерти или сникерс? Разумеется жизнь в раю после смерти! А что вообще может быть круче жизни в раю после смерти? Да нет ничего круче! Но сникерс лучше, чем ничего, а раз так, то он круче, чем жизнь в раю после смерти!
Между прочим, на нарушениях закона тождества плодятся не только одни софистические высказывания. С их помощью можно неплохо пошутить в литературном произведении! Возьмем, к примеру «Мертвые души» Николая Васильевича Гоголя. С нарушением логического закона тождества автор описывает Ноздрева, как «исторического человека». Почему? Да потому, что где бы он ни появлялся – с ним непременно происходила некая «история».
В афоризмах также нередко нарушается закон тождества: «Не стой где попало, а то еще попадет». Не забывают о таком приеме и авторы анекдотов:
– Я проломил себе череп в трех местах.
– Лучшие не ходи в такие места.
– В вашем отеле имеются номера, где тихо?
— В наших номерах везде тихо, что не скажешь о шумных постояльцах
– Вовчик, а ты нырнуть прямо сейчас в воду смог бы?
– Смог бы.
– И как долго сможешь не всплывать?
– Да пока меня из воды не выволокут.
– Эх, какие мечты в детстве были. Твои хоть какие-то сбылись?
– Ну да. С детства не любил парикмахера и мечтал никогда к нему не ходить.
— Ага, с лысой башкой это не к чему.
– Вова! Почему опаздываем на первый урок?
– Мне хотелось отправиться порыбачить с папой, однако меня не взяли.
– Отлично! Папа же тебе сказал, отчего ты должен предпочесть занятия рыбной ловле?
– Конечно. Он решил, что раз червей накопали только на одного рыбака, то второму с удочкой делать нечего.
Бабуля объясняет маленькому Вове почему алкоголь до 18 вреден:
– Да брось ты, дед всю жизнь пробухал – ни одного дня трезвым не видели! Вчера ему 80 лет исполнилось!
Бабуля находчиво отвечает:
– А не бухал бы – так ему и вовсе 90 было бы!
Экзамен. Суровый препод спрашивает:
– Фамилия, уважаемый?
– Сидоров.
– Что улыбаемся Сидоров?
– Радостно мне!
– Это ж почему?
– Так я уже на ваш первый вопрос ответил!
Лишь только деду нашему стукнуло 60 – он стал пробегать по 5 км в день. Сегодня ему за 80, и мы даже представить не можем где он бегает.
– Доченька! Твой жених хром на обе ноги, косит левым глазом, правый не видит… Родных у него нет – умерли давно. Безработный к тому же. Не выходи за него!
– А не нужен мне принц на белом коне – красивый или богатый. Я в любовь верю!
– Эх, не про то я. Парнишка этот и так в жизни горя хлебнул, а тут еще ты на его шее повиснешь…
Нарушение закона тождества – лучший конструктор для головоломок и задач на развитие интеллекта. Вот одна из них: спросите своего друга: «Зачем (на самом деле — «за чем»!) находится вода в стакане из стекла?» Этим вопросом мы специально моделируем ситуацию с двумя смыслами. С одной стороны «зачем» – подразумевает «для чего», с другой под «за чем» мы хотим узнать за каким именно веществом или предметом спрятана (находится) вода. Добровольный участник вашего коварного эксперимента обычно на озвученный выше вопрос отвечает не задумываясь, что-то вроде: «Зачем? Ну, чтоб пить. Чтобы цветочки орошать». Мы же говорим ему гордое «нет! Не угадал!» и всеми правдами и неправдами пытаемся выдавить правильное решение головоломки. Он должен ответить: «За стеклом!».
Подводя итог главы, отметим, что для соблюдения закона тождества, изначальные мысли по ходу рассуждения не нужно менять. Для практического его применения всего-то и нужно, что вступая в дискуссию или составляя речь – стараться четко представлять предмет рассуждения. Это даст возможность уйти от ненужных двусмысленностей и потери первоначального смысла.
Конечно, закон тождества совсем не указывает на то, что есть в нашем бренном мире вещи извечные, неподверженные никаким изменениям. Он не настолько глобален. Его смысл в том, что человеческая мысль, помещенная в рамки языковой фразы, останется тождественной себе даже с учетом некоторых речевых преобразований.
II. Закон исключенного третьего, или третий лишний
Это, пожалуй, наиболее известный из всех законов логики Аристотеля, который особенно прославила и растиражировала по свету латинская фраза «tertium non datur» (или третьего не дано). В чем суть закона исключенного третьего? Все просто. Если о предмете утверждается какая-та истина (первое суждение), и если кем-то эта истина опровергается (второе суждение), то только одно из них должно быть верным – третьему путь заказан!
«…нет ничего посреди меж двух противоречивых суждений об одном, — в Третьей Книге «Метафизики» отмечал Аристотель, — всякий отдельный предикат следует либо отрицать, либо утверждать». Греческий философ очерчивал границы применения закона третьего лишнего. По его словам, использовать его можно было только в разговорах о прошедшем и настоящем времени. Табу на применение правила накладывалось только на будущее время, так как сложно уверенно утверждать состоится то или иное событие или нет.
Очевидно, что закон непротиворечия и закон исключенного третьего тесно связаны. Действительно, те суждения, которые подходят под действие закона исключенного третьего, подходят и под закон непротиворечия, но не все суждения последнего, попадают под действие первого.
Ниже мы приведем несколько формул, в которые можно вписать закон исключенного третьего:
А) «X не есть Y» и «Y есть X»
Суть формулы: Одно и тоже суждение отрицает нечто о предмете в определенном отношении и определенном времени, при этом второе суждение тоже самое утверждает. В качестве примера: «Медведи – грызуны» и «Медведи – не грызуны».
Б) «Некоторые X не есть Y» и «Все X есть Y»
Суть формулы: Некое суждение утверждает нечто по отношению ко всему классу предметов, при этом второе суждение это отрицает, однако по отношению только к некоторой части этих предметов. В качестве примера: «Все солдаты Западного фронта получили медаль за отвагу» и «Отдельные солдаты Западного фронта получили медаль за отвагу».
В) «Некоторые X есть Y» и «Ни одно X не есть Y»
Суть формулы: Определенное суждение полностью отрицает наличие характеристики у класса вещей, при этом второе суждение такую характеристику утверждает, однако — в отношении лишь части этих предметов. В качестве примера: «Ни один житель нашего дома не пользуется Интернетом» и «Некоторые жители нашего дома пользуются Интернетом».
Этот закон Аристотеля в свое время был подвержен критике со стороны других философов. Особенно стали цепляться к нему во времена Новой истории. Все злопыхания можно свести к словесной формуле следующего типа: «Можно ли с полной уверенностью считать всех лебедей мира черными, отталкиваясь лишь от такой посылки, что до сих пор нам попадались на глаза лишь птицы этого цвета?». То есть, ученые считают, что зачастую закон Исключенного третьего применим только в двузначной, основанной на абстракции, логике Аристотеля. А так как в реальной жизни ряды элементов теряются в бесконечности – исключить все возможные альтернативы очень сложно. Поэтому приходится задействовать иные логические принципы.
Закон исключенного третьего плотно взаимодействует с еще одним законом логики Аристотеля — законом непротиворечия. И о нем – ниже.
III. Закон непротиворечия, или обойдемся без пожилых детей
Очередной формальный закон логики утверждает, что оба друг с другом несовместимых суждения не способны в одно и тоже время оказаться верными – среди них имеется хотя бы одно ложное. Закон непротиворечия таким образом словно следует из закона тождества. «Это нереально, чтобы нечто в одно время было присуще, а также не было присуще чему-то…, — утверждал в своих трудах Аристотель. Чтобы лучше понять мысль известного грека, обратимся к примерам. Ниже приведем две взаимоисключающие фразы:
А) Всякий, кто зашел на интернет-ресурс iq230.com – закончил университет с красным дипломом.
Б) Никто из посетивших интернет-ресурс iq230.com не закончил университет с красным дипломом.
Логика поможет нам разобраться в том, какое из представленных суждений истинное, и есть ли истинность в них вообще. Изучив фразы А и Б, мы способны предположить, что обе они в одно и тоже время не способны оказаться истинными, так как на лицо явное противоречие. Из этого следует сразу несколько важных вещей. Во-первых, если удастся доказать, что одно из них истинно, следовательно второе будет ложным. Во-вторых, если мы докажем ложность одной из фраз, то вторая с одинаковой долей вероятности может оказаться и истинной, и ложной. Соответствующего опроса наш ресурс среди посетителей не проводил, но если вдуматься, то оба представленных выше утверждения должны показаться вам ложными.
Закон непротиворечия (противоречия) ставит запрет на одновременное утверждение и отрицание чего-то одного. С одной стороны это правило кажется на 100% очевидным и даже возникают сомнения в необходимости формулировки такого очевидного закона логики. Но не все так просто. Необходимо изучить условия, при которых данный принцип нарушается.
Так, к примеру, нарушение закона непротиворечия произойдет в случае, если две последующие фразы будут произнесены с учетом современных реалий российской действительности («Санкт-Петербург не является столицей Российской Федерации» и «Санкт-Петербург является столицей Российской Федерации»). Другое дело, если оба эти утверждения звучат не в едином контексте, а относятся к разным эпохам. В таком случае все верно: Сегодня Санкт-Петербург и в самом деле не является столицей Российской Федерации. При этом город на Неве являлся столицей, если речь идет в русле событий 18 века.
Вот еще один красноречивый пример аналогичного казуса. «Я отлично говорю по-французски», а также «Я посредственно говорю по-французски». И то и другое утверждение могут оказаться верными, если речь в них идет о разных вещах. Например, в университете я сдал экзамен по французскому языку на отлично, следовательно — я отлично говорю по-французски! Обрадованный, я пошел устраиваться в контору переводчиком, а там меня зарубили на тестировании – для работодателя мой уровень владения языком оказался недостаточным. Вывод? Я посредственно говорю по-французски!
Контактные противоречия в логике. Примечательны они тем, что встречаются крайне редко, но если звучат из речи политиков, то на них тут же обращаешь внимание. Когда возникают контактные противоречия? Происходит это когда практически одновременно нечто называется ложным, а затем – буквально в следующем предложении – истинным.
Дистантные противоречия в логике более распространены. Суждения подобного рода (также диаметрально противоположные) звучат не одно за другим, а спустя определенное время. Нужно постоянно следить за тем, чтобы не сбиться с первоначального пути. Такую ошибку зачастую допускают начинающие журналисты и научные работники. Хотите примеров?
Вот небезынтересный ляп из учебника по литературе. С интервалом в несколько страниц в нем утверждались две взаимоисключающие вещи «Уже с самого начала своего творчества Маяковский обладал качествами, которые существенно отличали его от представителей футуризма» и вот еще «В первый период творчества Маяковский ничем не отличался от футуристов».
При этом противоречия бывают также неявными и явными. В первом случае противоречие следует из контекста фразы, словами оно не сформулировано, однако подразумевается. Во втором же — одна мысль непосредственно противоречит другой. Явных контактных противоречий не так много в повседневной жизни – другое дело симбиоз неявных с дистантными.
Неявные противоречия, как и дистантные, в силу своей незаметности намного более распространены в мышлении и речи. Явные противоречия (также как и контактные) наоборот — встречаются редко. Их примером могут послужить следующие фразы:
Таксист при выезде со стоянки нарушил правило, так как не соизволил взять устного разрешения в письменной форме.
Юная особа престарелого возраста с еле заметным ежиком рыжих волос до пояса, изящно прихрамывая, предстала перед публикой.
Столь очевидные противоречия часто применяются юмористами и литераторами для придания комического эффекта. А вот другие группы противоречий, уже не столь явные, больше напоминают ошибки и с ними нужно бороться. Вот пример такого «ошибочного» неявного и одновременно контактного противоречия «Данная рукопись создана в XI веке на Руси». Ничего подозрительного не заметили?! А подозрительное есть! В этот период времени на Руси еще не было писчей бумаги!
Не забудем упомянуть и про мнимые противоречия. Говоря кратко – это особенная смысловая (речевая) конструкция, только кажущаяся противоречивой, но на самом деле таковой не являющаяся. «В детстве у меня не было детства», — поговаривал Антон Павлович Чехов, вспоминая юные годы. Если постараться разобрать эту фразу не вникая, то можно предположить, что известный прозаик утверждает две диаметрально противоположные вещи: с одной стороны у него есть детство, а с другой – нет. Это мнимое противоречие и закон непротиворечия здесь не нарушен, так как речь в высказывании Чехова идет не об одном и том же предмете в одно и тоже время: с одной стороны – это определенный возраст, с другой – состояние души, время особого счастья и безоблачной радости. Такое мнимое противоречие специально используется Чеховым. С его помощью он достигает наилучший художественный эффект.
Мнимое противоречие – прием, который с удовольствием использовали и используют сотни известных авторов литературных произведений. Его можно даже в названии классических произведений найти! У Льва Николаевича Толстого было замечательного произведение «Живой труп», у Александра Сергеевича Пушкина – «Барышня-крестьянка». Подобных произведений в мировой литературе масса: «Мещанин во дворянстве», «Горячий снег» и т.д. Журналисты таким приемом тоже не брезгуют: «Нищий олигарх», «Родной враг», «Честный жулик»…
Особенно хороши мнимые противоречия в афоризмах:
Эйнштейн: Самое непостижимое в мире кроется в том, что он постижим
Сократ: Я знаю лишь то, что ничего не знаю
Пушкин: Слышу умолкнувший звук божественной эллинской речи
Гегель: История учит только тому, что она ничему не учит
Подводя итог, отметим, что закон противоречия (непротиворечия) «специализируется» на связях между логическими противоречиями (двумя противоположными по смыслу суждениями), совершенно не затрагивая противоположных граней единого предмета. Знание такого закона и следование ему дисциплинирует мыслительную деятельность и позволяет избегать досадных ошибок.
IV. Закон достаточного основания, или Полнота доказательств
Вот мы и добрались до 4-го формального закона логики. И так вышло, что вывел его не Аристотель, а математик и философ Готфрид Лейбниц в научном труде «Монадология» (1714 год). В своей работе немецкий ученый подчеркнул «…ни одно из существующих явлений не будет действительным или истинным, и ни одно утверждение не будет справедливым без достаточного основания, без указаний почему дело обстоит именно так, и никак по другому (пусть даже такие основания в большинстве случаев не могут быть нам известны)».
Более приближенный к нам во времени Готфрид Лейбниц считает, что для того, чтобы называться достоверным, любое положение необходимо доказать. А для этого необходимы основания, причем – в полном объеме. То есть, закон достаточно основания напоминает логику о необходимости быть обоснованным в своих суждениях.
Своим вкладом в логику Готфрид Лейбниц связал законы Аристотеля и условия их определенности, непротиворечивости, а также последовательности и рассуждения. Известный математик намекает, что в действительности одного лишь истинного суждения недостаточно. В практической жизни или познавательной деятельности людям этого мало – нужно уметь обосновывать свою позицию.
Закон достаточного основания применяется нами регулярно. Всякий раз, когда мы делаем выводы, используя для этого основание (факты) – мы совершаем то, о чем говорил Лейбниц три века тому назад. Обычное дело, когда научный работник в конце своей кандидатской или докторской диссертации помещает «список использованной литературы». Этим он подкрепляет основную идею своего исследования и работает в русле закона достаточного основания.
Не обязательно быть деятелем науки, чтобы применять правило Лейбница в повседневной жизни. Этим занимаются чуть ли не все российские граждане: школьники, студенты, журналисты, а уж как востребован закон достаточного основания в судебной сфере! При подготовке обвинительного заключения или позиции защиты без него никуда.
Интересно, что часто закон Лейбница нарушают, причем – и не только в связи с неграмотностью отдельных людей. Иногда это делается, чтобы обвести собеседника вокруг пальца. Например: «Сергей полностью здоров, так как у него не течет из носа» или «Чикатило Чикатилович не способен расчленять маленьких девочек, ведь все его знают в качестве ударника труда, замечательного мужа и отца». Не нужно быть семи пядей во лбу, чтобы узнать, где аргументы в представленных выше фразах недостаточно обосновывают основное утверждение.
Ниже представлены некоторые формы нарушения рассматриваемого нами закона логики:
— Миша обсолютно здоров, так как он подтянулся больше всех в классе
— В Костромской области пьяные охотники съели снежного человека и это правда, ведь про этот факт трезвонили во всех местных газетах
— Ты виноват уж тем, что хочется мне кушать (цитата из басни Крылова)
Водой успешно уничтожают пожары по причине, что она текучая и ее температура ниже, чем у огня.
Тот, кто соблюдает закон достаточного основания, успешно избегает в своих выводах скорых, необдуманных утверждений, голословных фраз. Здесь уже нет места для слухов, басенок и сплетен. Закон достаточного основания позволяет избегать любых мистификаций и неплохо отражается в поговорках:
Доверяй, но проверяй
Язык без костей
Не верь своим глазам (вариант – «ушам»)
Говорят так, словно кур доят
Никакому интеллектуальному мошенничеству не обойти закон достаточного основания! Он дает запрет на слепую веру в чудеса и зримо разграничивает истинную науку от псевдонауки (астрология, нумерология, алхимия и много других).
Так как любая лженаука старается выглядеть солидно (даже прикрываясь авторитетом истинных научных дисциплин) – настоящим ученым просто необходимо пользоваться законом достаточного основания. В его русле ученые и стараются работать, опираясь на важнейшие принципы:
1. Принцип верификации (термин имеет латинское происхождение от слов Veritas и facere, которые переводятся как «истина» и «делать») предписывает понимать под научным лишь знание, истинность которого есть возможность подтвердить – раньше или позже, прямо или косвенно. Еще в 20-м веке англичанин и философ Бертран Рассел предложил руководствоваться этим принципом.
К сожалению, сегодня псевдонауки настолько поднаторели в запудривании мозгов, что складывается впечатление, словно все их доводы легко подтверждаемы. Поэтому в помощь принципу верификации ученое сообщество добавило и принцип фальсификации. Его предложил в свое время другой (уже немецкий) философ 20-го века Карл Поппер.
2. Принцип фальсификации (термин имеет латинское происхождение от слов false и facere, которые переводятся как «ложь», «делать») утверждает, что лишь такое знание считается научным, которое можно опровергнуть – раньше или позже, прямо или косвенно.
Не звучит ли для вас определение принципа фальсификации не совсем логичным. Неужели подлинное научное знание – то, которое опровергается? Как бы ни звучало это дико, но все обстоит именно так. Современная наука не стоит на месте, практически все теории со временем опровергаются новыми. Для движения вперед важна не одна лишь подтверждаемость научной мысли, но и возможность ее опровергнуть. Примеров можно привести массу. Древние, к примеру, считали, что Земля – центр вселенной, а Солнце и звезды кружатся вокруг нее. Вера в это сохранялась 2000 лет! Исходя из этого убеждения, ученые совершили массу «открытий». Теперь это представление считается устаревшим и все наработки того периода опровергнуты. Лишь в 15 веке человечество пришло к мысли, что это Земля кружится вокруг Солнца, а не наоборот.
Если один из представленных выше принципов (верификации) адепты псевдонаук еще могут обойти, но испытание принципом фальсификации они пройти не могут. Тот, кто исповедует псевдонауку, согласится с тем, что все в его «научной дисциплине» подтверждается фактами, но он никогда не признает, что со временем это может быть опровергнуто новым знанием. Он считает, что его древняя наука, впитавшая в себя мудрость веков – абсолютно верна, непогрешима и неопровержима. Так что если кто-то однажды скажет вам, что его научное знание неопровержимо, будьте уверены – вы имеете дело с последователем лженауки. Настоящий ученый легко признает, что теория, которой он, возможно, посвятил многие годы своей жизни, со временем может быть опровергнута другими исследованиями.
В отличие от серьезных научных дисциплин псевдонаука не развивается, а стоит на месте. Все ее выводы и теории – неизменны с момента зарождения, что роднит лженауку с деятельностью диких шаманов и колдунов.
Тренировка Логического мышления
1) Скажите, какой закон формальной логики нарушен:
(Наследие Гоголя)
Один там только и есть порядочный человек: прокурор. Да и тот, если сказать правду, свинья»
(Наследие О.Хайяма)
Дураки мудрецом почитают меня,
Видит Бог: я не тот, кем считают меня.
О себе и о мире я знаю не больше
Тех глупцов, что усердно читают меня
(Наследие Мольера)
— Конечно, Вы хотите написать ей стихи?
— Нет, нет, только не стихи.
— Вы предпочитаете прозу?
— Нет, я не хочу ни прозы, ни стихов».
2. Какая из представленных внизу фраз может стать основой для еще одной из этого списка:
— Иванов не станет смеяться над пошлой шуткой.
— Иванов, как правило, не сеется над пошлыми шутками.
— Иванов вряд ли станет смеяться над данной шуткой.
3. Можно ли сказать, что в представленной ниже фразе нарушается закон исключенного третьего:
Про Иванова не скажешь, будто этот человек бездельник и лентяй. Также не стоит говорить, что он не бездельник и не лентяй
4. Взяв на вооружение закон непротиворечия, скажите, являются ли представленные ниже фразы одновременно истинными и почему:
В лесу все березы покрылись почками. Не все березы в лесу покрылись почками.
В лесу все березы покрылись почками. Многие березы в лесу покрылись почками.
Очень немногие школьники 3-го А осилили этот диктант. Ни одному школьнику 3-го А не удалось осилить этот диктант.
Есть люди, которые поучают большое удовольствие от чтения Толстого. Есть люди, которые не получают большого удовольствия от чтения Толстого.
5) Скажите, какой закон формальной логики нарушен:
Все пожарные знают как эффективно тушить пожар. Иванов знает, как эффективно тушить пожар, значит он — пожарный.
Маруся посетила доктора философии, чтобы он выписал ей лекарство от гриппа.
6) А теперь, уважаемые читатели, постарайтесь сами придумать пару-тройку примеров, в которых формальные законы логики безбожно нарушаются.
5-10. Математические законы логики: Клавия, Пирса, де Моргана и др.
Ниже мы рассмотрим более сложные, в основном применяемые в сферах математики законы логики. Чтобы не перегружать читателя сложной информацией с обилием математических формул, мы свели соответствующие формулировки и определения к минимуму.
Закон двойного отрицания
Еще один из важнейших принципов классической логики — закон двойного отрицания утверждает следующее: «если неверным считается то, что неверно А, то следовательно А — верно». Альтернативное название для этого логического закона — закон снятия двойного отрицания.
Особое распространении логический закон двойного отрицания имеет в традиционной содержательной математике, где он является веским доводом к проведению доказательств от противного. Такие доказательства проходят интересным образом. Первым делом из некого предположения о том, что определенное суждение А не является верным, выводится противоречие в конкретной теории. Затем на основании непротиворечивости теории появляется вывод, что в действительности неверным является «не А». В результате по закону двойного отрицания делается вывод о том, что А верно.
Отметим, что при конструктивных рассмотрениях в математике закон двойного отрицания оказывается неприемлем, особенно если имеет место требование алгоритмической реализуемости обоснования математических суждений.
Стоит подчеркнуть, что закон двойного отрицания плотно взаимодействует с законами Пирса и исключённого третьего. В какой-то степени всю эту троицу можно расценивать, как эквивалентную друг другу. Некоторые философы даже выводят их один из другого.
Закон Клавия
Очередной закон логики – закон Клавия объединяет отрицание и импликацию (которая обычно выражается формулировкой «если, то»). Этот принцип разработал математик-немец Христофор Клавий, впервые упомянувший его в своей научной работе, посвященной евклидовой «Геометрии». Напомним, что античный философ доказал одну из своих теорем, допустив, что она не верна.
Принцып закона Клафия: если некоторое утверждение является следствием своего отрицания, то оно (данное утверждение) является истинным.
Закон контрапозиции
Этот закон классической логики настаивает на том, что при условии, если некоторая посылка A влечёт за собой некое следствие B, то отрицание данного следствия (иными словами «не B») влечёт отрицание такой посылки (иными словами «не A»). Закон контрапозиции, как и закон двойного отрицания, наибольшее применение получил в математических выражениях.
Закон Пирса
Закон Пирса принято расценивать, как своеобразный аналог сразу нескольких законов классической логики: исключенного третьего и двойного отрицания. Свое название он получил в честь Чарльза Пирса, логика и философа из США.
Закон Пирса сформулирован следующим образом:
P должно быть истинным, если следование Q из P с необходимостью влечёт P. Данный логический принцип принято считать тавтологией классической логики и аналогом законов исключенного третьего и двойного отрицания. Многие философы говорят об эквивалентности всех трех законов.
Правила (законы) де Моргана
Законы де Мо?ргана это такие логические правила, которые посредством логического отрицания объединяют пары логических операций. Свое название они получили в честь Огастеса де Моргана, выдающегося математика из Шотландии. Вкратце законы де Моргана можно представить двумя формулами:
Отрицание дизъюнкции есть не что иное, как конъюнкция отрицаний
Отрицание конъюнкции есть не что иное, как дизъюнкция отрицаний
Правила де Моргана особо распространены в электромеханике, дискретной математике, физике. В информатике они применяются с целью оптимизационных работ с цифровыми схемами через замену логических элементов другими логическими элементами.
Законы деления (дихотомия логики)
Логические законы деления существуют для эффективной систематизации и соответствующей классификации различных предметов или явлений. При этом в делении применяются важнейшие принцыпы:
необходимость соразмерного деления
предметам деления следует друг друга исключать, иными словами они не должны пересекаться между собой
на всех своих этапах деление необходимо производить только по одному основанию
следует исключить скачкообразное деление
При делении объема понятия иногда допускаются ошибки:
• понятие делится в неполном объеме;
• деление чересчур обширно;
• логическая ошибка, возникающая в связи с нарушением правила о необходимости непрерывного деления (ошибка называется «скачок в делении»)
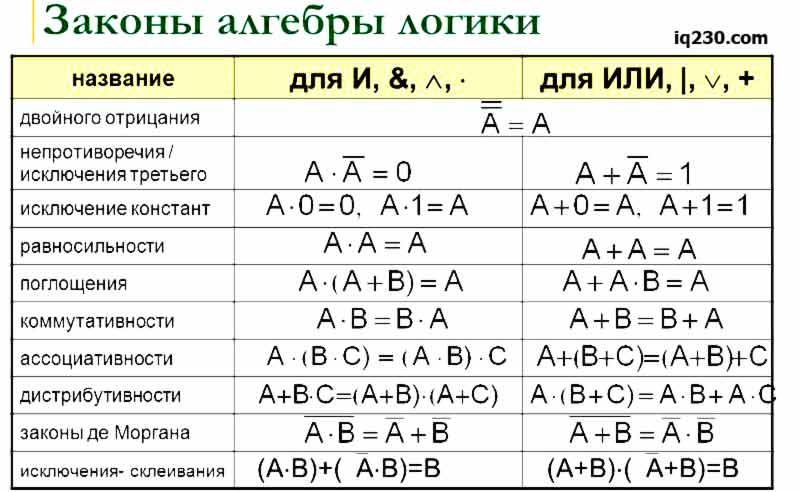
Ниже представлена таблица с формулами основных логичесских законов.
