Нам предстоит изучить только лучшие способы перемножения двухзначных чисел. Статья содержит наиболее распространенные и потому эффективные приёмы. В результате они позволят вам научиться умножать двухзначные числа в уме в разы быстрее.
Способ №1 – разложение числа на десятки и единицы
Наиболее легким и понятным является методика перемножения двухзначных чисел из школьной программы. Суть этого способа заключается в разбиении множителей на десятки и единицы. Далее получившиеся четыре числа перемножаются между собой. Метод простой, но для его использования необходимо умение запоминать одновременно несколько числовых значений и производить с ними арифметические расчеты.
Например: 54*73 = (50+4)*(70+3) = 50*70 + 50*3 + 4*70 + 4*3 = 3500+150+280+12 = 3942
Проще всего подобные примеры решать в три действия. В первом действии перемножаются десятки, во втором — единицы с десятками и суммируются между собой, а в третьем действии к полученной сумме прибавляется произведение единиц.
Это выглядит так:
1. 50*70 = 3500 – запомнить в уме
2. 50*3+4*70 = 430 – запомнить в уме
3. (3500+430)+3*4 = 3942 – итоговый результат
Для того чтобы за максимально короткое время решать такие примеры, необходимо обладать достаточно прочными знаниями таблицы умножения и уметь суммировать однозначные и двузначные числа, а также обладать способностью быстрого переключения внимания между производимыми расчетами, запоминая их в уме. Этот навык можно натренировать с помощью визуального представления совершаемых арифметических вычислений. Как он осуществляется? При помощи представления картинки вашего решения и получившихся промежуточных результатов.
Как видно из примера, эту методику умножения нельзя назвать самой простой и эффективной, поэтому следует иметь в виду и другие, альтернативные ей способы.
Способ №2 – арифметические подгонки
Среди вариантов вычислений в уме этот способ можно считать одним из наиболее распространенных. Подгонка примера применяется в случае, если необходимо быстро вычислить примерный или точный результат. Этот способ наиболее широко применяется в школах и высших учебных заведениях с математическим уклоном. Школьников и студентов обучают искать наиболее простые алгоритмы вычислений. Далее представлено несколько примеров таких подгонок:
Подгонка примеров к соответствующему виду считается очень популярным способом подсчетов в уме. Она применяется, когда вам требуется в короткие сроки определить приблизительный или правильный ответ. Школьников и студентов обучают искать наиболее удобные алгоритмы вычислений для разнообразных задач. Варианты подгонок представлены ниже:
Пример 49*49 решается следующим образом: (49х100) / 2 — 49. В первую очередь 49 умножается на сто – 4900. Потом 5900 делится на два – 2450. Из полученного результата вычитается 49. В итоге получается 2401.
Произведение чисел 56х92 вычисляется следующим образом: 56х100-56х2х2х2. Из этого следует: 56х2 = 112х2 = 224х2 = 448. Далее из 5600 вычитается 448, получается 5152.
Подобный вариант решения может быть применим только тогда, когда вы способны в уме умножать двузначные и однозначные числа и запоминать все полученные результаты. Помимо этого, приходится постоянно подбирать правильный алгоритм решения каждого примера и следить за его соблюдением.
Вывод. Этот способ отлично подходит для тренировки умственных способностей и памяти, но вероятность получить неверный результат из-за неправильно выбранного алгоритма решения значительно выше, чем при применении способа №1.
Способ №3 — визуальное представление в уме перемножения в столбик
56х67 – произведем расчеты в столбик.
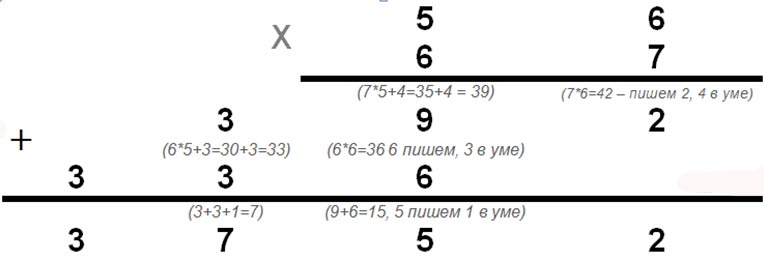
Сложность такого умножения заключается в необходимости постоянно держать в памяти несколько вспомогательных чисел, а количество арифметических действий значительно больше, чем у других методов. Но произведение расчетов можно сделать значительно проще. В ЭТОЙ статье мы говорили о важности умения быстро перемножать однозначные числа с двузначными. Если вы уже научились это делать, то вычислить в столбик в уме для вас не составит труда. Порядок действий следующий:
1. 56х7=350 + 42 = 392 – запоминаем.
2. 56х6 = 300 + 36 = 336 — запоминаем.
3. 336х10 + 392 = 3360 + 392 = 3752 – это уравнение сложнее, но вычисление можно сделать проще путем проговаривания числа, которое не вызывает у вас трудностей. Пока вы проговариваете, суммируйте 360 и 392.
В итоге мысленные вычисления в столбик напрямую сложны, но можно значительно упростить этот процесс, если натренировать способность быстрого перемножения двузначных и однозначных чисел. Проще говоря, умножение в столбик является более сложной вариацией способа №1. Что лучше – выбирать вам.
Главным плюсом 3-х способов перемножения двухзначных чисел для устного счета в уме, приведенных выше, является их универсальность — они могут применяться для различных вычислений. Имея достаточно навыка устных вычислений, и зная эти способы, вы сможете найти правильное решение соответствующей задачи. Но при использовании правильных алгоритмов решения, можно значительно сократить количество выполняемых при решении в уме действий.
Способ 4. При умножении на 11
Наиболее простым является умножение любого двухзначного числа на 11. Для вычисления между первыми двумя цифрами множителя, отличного от 11, ставится сумма этих чисел.
Например, при умножении 14 на 11,между 1 и 4 вставляем сумму этих чисел (1+4). В итоге получается: 14*11 = 1 (1+4) 4 = 154.
Если центральные цифры в сумме дают результат больше десяти, то к первой цифре следует добавить единицу, а вторую цифру надо заменить суммой цифр умножаемого числа с вычетом 10.
Например: 56*11 = 5 (5+6) 6 = 5 (11) 6 = 616.
Этот способ можно использовать для умножения на 11 любых двухзначных чисел. Можно привести дополнительные примеры:
73 * 11 = 7 (7+3)3 = 803
45 * 11 = 4 (4+5) 5 = 495
Быстро производить умножение двухзначных и любых других чисел на одиннадцать в уме легко.
Формулы сокращенного умножения: квадраты суммы и разности
Для возведения в квадрат двухзначных чисел хорошо подходят формулы квадратов суммы и разницы.
К примеру:
142= (10+4)2 = 102 + 4*2*10 + 42 = 100+80+16 = 196
782 = (80-2)2 = 802 – 80*2*2 + 22 = 6400-320+4 = 6084
Способ 5. Возведение в квадрат чисел, которые заканчиваются на 5
Числа, заканчивающиеся на пять, возводятся в квадрат по очень простому алгоритму. Числа до конечной 5-ки умножаются на это же число, и добавляется единица. К оставшемуся числу прибавляется число 25.
352 = (3*(3+1)) 25 = 1225
452 = (4*(4+1)) 25 = 2025
752 = (7*(7+1)) 25 = 5625
Такой же алгоритм применяется для более сложных примеров:
3552 = (35*(35+1)) 25 = (35*36)25 = 126025
Способ 6. Умножение чисел до 20
Этап № 1. В качестве примера будем использовать числа 15 и 19. К одному из чисел добавляем количество единиц другого. Получаем: 15+9=24
Этап № 2. Полученное число нужно умножить на 10. Получаем: 24*10=240
Этап № 3. Далее получившееся число складываем с произведением единиц 15 и 19 – 240+5*9=285
Данный пример можно «сократить» в записи:
15*19 = (15+9)*10+5*9 = 285
Доказать верность этого метода можно следующим образом: 15*19 = (10+5)*(10+9) = 10*10+10*5+10*9+5*9 = 10*(10+5+9) +5*9.
Фактически этот метод представляет собой способ применения для расчетов опорных чисел. В конкретном примере опорным числом является десятка. Последнее выражение наглядно показывает, что именно на это число мы и умножали расположенное внутри скобки. Вместо десяти опорным числом может выступать и любое другое число. Наиболее удобными принято считать числа 100, 50, 25 и 20. В ЭТОЙ статье более подробно рассматривается использование опорных чисел. Здесь же приведем только ознакомительное описание этой темы.
Применим методику опорного числа для перемножения чисел 14 и 16. Тут, так же как и в прошлом примере, удобнее будет использовать 10-ку как опорное число. 14 больше десяти на 4, а 16 – на 6. Для определения произведения этих чисел нужно произвести следующие действия:
К одному из множителей прибавляется число, на которое второй множитель больше опорного. А именно, 6 — к 14, или 4 — к 16 (не делайте этого одновременно!). В обоих случаях получается одно и то же: 20. Затем 20 умножаем на опорное число, то есть на 10. Результат: 200.
К 200 прибавляем произведение 4*6. Ответ: 224.
